固定收益这一块，很多人都认为很难，但实际如何呢？据统计，得分率却相对不低。因为它属于非常有逻辑和章法的内容，只要足够花心思去理解，尤其是掌握好几大难点，还是很容易在考场上拿分的。
上周，我们也是开启了固收这门课的学霸笔记，不知道小伙伴们有没有每周跟着我们学习一个知识点呢？错过的可以戳下面的文章链接跳转哦
今天小妞就接着聊聊久期的好伙伴——凸性（Convexity）。
本来简简单单一条直线为啥非得掰弯？
话说凸性这个概念出现之前，评判某支债券的利率风险，也就是债券价格随着收益率变化的关系，是用久期这个概念来衡量的。人们在麦考林久期的基础上得到了修正久期，作为斜率因子来反映“价格-收益率”这条直线的陡峭程度，也就反映出价格随利率变化的快还是慢。
但这个久期有个缺点是只适用于普通债券，对含权债券比如可赎回债券（callable bond）等等就会明显出错。人们很奇怪，干脆通过已有数据来观察利率变动对价格的影响，反推出久期的大小（也就是有效久期），结果发现，很多债券在不同的价格/利率变动区间有不同的久期结果；也就是说债券价格与收益率确实呈现反向关系（久期为负），但是这个关系往往不是斜率恒定的简单直线，而是一条曲线！
这就非常头痛了，因为久期本身会随着利率的变化而变动，这就意味着仅用久期无法作为一个恒定的属性来描述债券本身的利率风险！
当然，如果利率只是小幅波动，那么久期还是可以较好地衡量价格变动；如果利率大幅变动，那么仅仅用直线无法准确抓住利率改变对价格造成的变动。我们需要使用真正的曲线、需要考虑斜率本身的变化。这个时候，曲线的曲度（curvature）——斜率的变化率（一阶导）就被引入了。
微积分不好，
我是不是就得讨厌凸性？
说到这里，大家应该会有个“不祥的预感”：这个“曲度”，就是咱们债券世界的凸性吧……是滴！凸性本尊，说白了就是久期对利率的敏感程度，即有效久期的一阶导。那么根据有效久期，我们可以得到有效凸度的公式：
这是个啥？嗯，这就是个债券价格对利率求二阶导。微积分不好的同学也莫慌，大家知道有效久期是一阶导，那么凸性当然就是对导数再求导的二阶导啦。
而且凸性是个很单纯的存在，它不像久期那样种类多样，还各有各的经济含义——凸性本身并没有实际意义，只是与有效久期紧密相关，被视为对久期的补充，结合起来估计债券价格的变动、表现债券利率风险属性。
凸出来好还是凹进去好？
凹凸有致，确实是曲线美。凸性作为形容这种凹凸程度的一个数，在我们看债券-价格收益率曲线图的时候，尤其要注意：债券convexity“凸性”表现在图形上是朝坐标轴原点凸出，则凸性为正，越靠近原点越凸，凸性的数值越大。
如下图的price-yield curve(价格-收益率曲线)，我们可以直观感受一下这个曲线到底是凹进去的还是凸出来的？答案是：朝向原点凸出，凸性为正哦。
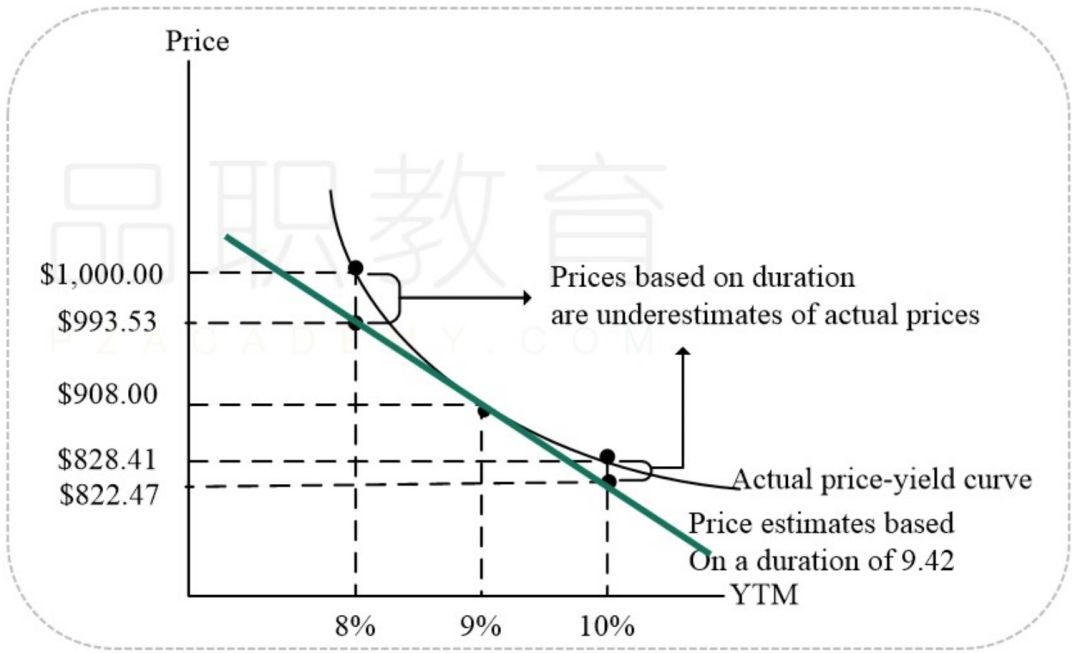
从上图中我们看到，由于久期可以看成利率的一阶导，随着利率上升，斜率变小即久期越小；当利率下降，斜率变大即久期越大。比如，当利率由9%下降到8%，债券价格实际上涨到1000美元，而用久期衡量则债券只增长到993.53美元；同样的，当利率由9%上升到10%，债券价格并没有到822.47美元，而是下降到828.41美元。
曲线与直线的距离之差就是由凸性造成的。这也是凸性具有的天然属性，即利率上升时债券价格变动相比仅用久期衡量要跌的少，而利率下降时债券价格变动又涨得更快，所以凸性这个“涨多跌少”的特性最受债券持有者喜爱。
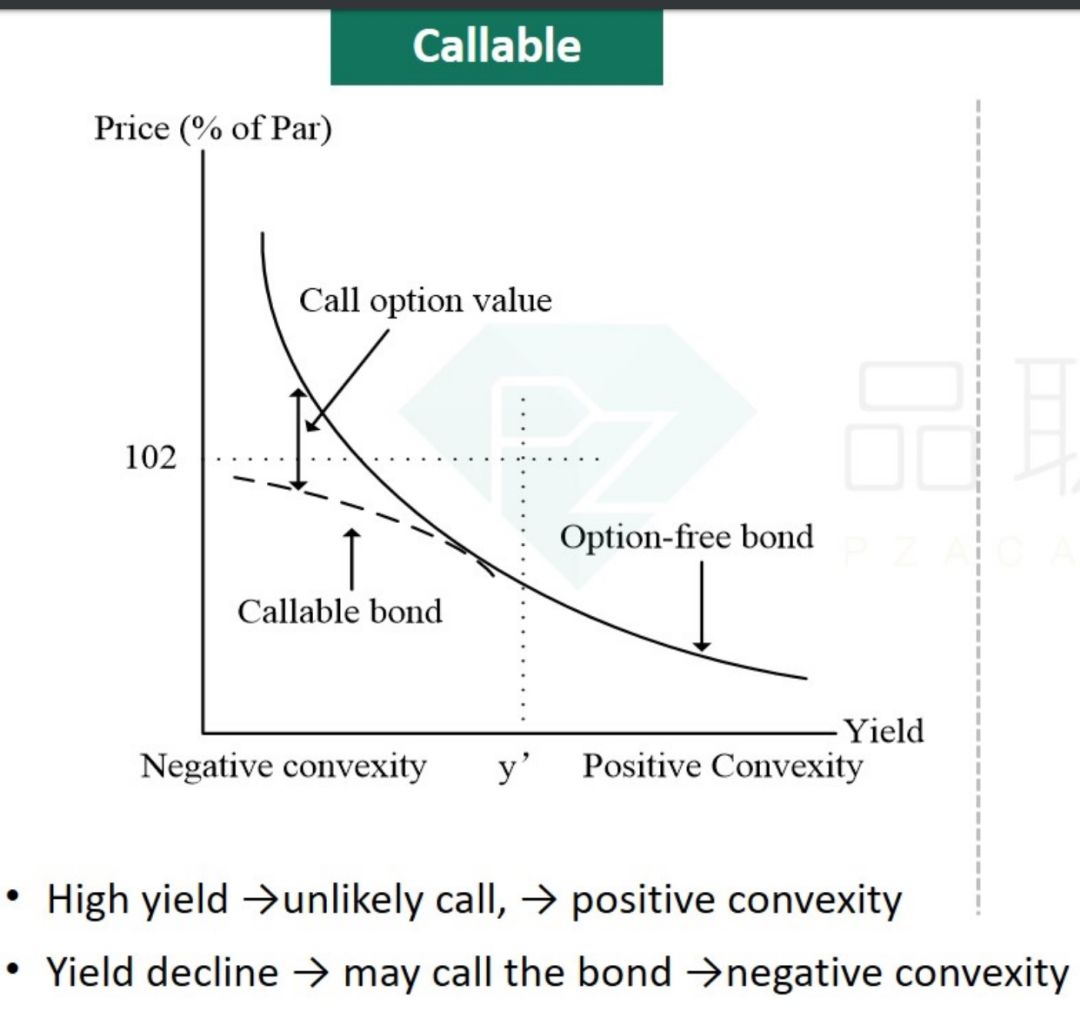
而对于可赎回债券（callable bond），其凸性可能会出现负凸（negative convexity）的情况。当利率下降到触发赎回条件时，债券发行人有权以约定价格（call price）从债券持有人手中赎回债券，此时可赎回债券的价格就不再上涨。
我们通过观察下图可以发现，普通债券的价格随着利率下降会上升，而可赎回债券的价格在到达102时就不会再增加也就是达到价格上限，此时价格与利率呈现一个凹向原点的形状，也就是负凸。但当利率上涨时，可赎回债券与普通债券一样，都呈现正常的凸性。
同样的，对可卖回债券（putable bond），当利率上升时，债券持有人有权以约定价格（put price）将债券卖给债券发行人，此时可卖回债券的价格就不再下降，从图形上看比普通债券的更加凸向原点，所以这种债券对投资人更有利。
债券各个参数之间的关系
凸性与久期一样，都会受到到期期限（maturity）、票面利率（coupon rate）和收益率（yield）的影响。那么，它们之间都有哪些微妙的关系呢？
Maturity越大→Duration越大→Convexity越大
由于久期与到期时间呈现线性关系，凸性又是久期的一阶导，所以凸性与时间呈现非线性的加速关系。
Coupon rate越大→由于还款期变短，Duration越小→Convexity越小
Yield越大→Duration越小→Convexity越小
小伙伴们，不用看到公式看到数学概念就头大啦，我们只要搞清楚概念之间你中有我、我中有你的关系，并不断练习加深理解、加快反应速度，一定会熟能生巧，轻松搞掂学习中的疑难杂症！
下周同一时间，学霸笔记继续陪伴大家哦！
戳原文，直接购买「2020品职CFA课程」
